Mareike Schmalz, Manager Battery Advanced Development, APL in Landau, Germany
Morten Kronsted, Manager Design and Simulation, APL in Landau, Germay
Dr. Marcus Gohl, Senior Manager Advanced Development, APL in Landau, Germany
The rapid transformation to climate-neutral mobility is only possible through accelerated design processes with increasing front-loathing. This gives simulation ever greater importance as an essential development tool. A key area of application is in batteries, from the establishment of new cell chemistries to the coherent overall system design. APL responds to the increasing complexity by tightly integrating simulation and testing environments. The following article takes a closer look at the challenges of battery development and the modeling approaches used in each case.
Necessity of battery simulation
The development objectives for traction batteries and their various system levels require a variety of modeling and simulation tools, Figure 1. Starting with conceptual design and basic layout the entire system must first be considered and dimensioned. This is best done using system simulations, as shown in the example in Figure 2. To predict the behavior of the battery system of a BEV while driving, a vehicle model with an integrated battery model was created. The parameterization and validation took place both via component tests on test benches and through vehicle investigations
under real driving conditions. Such an overall vehicle simulation allows the initial design of the electric powertrain in new systems. Furthermore, it forms the basis for revealing optimization
potentials and allows for benchmark comparisons to existing vehicles.
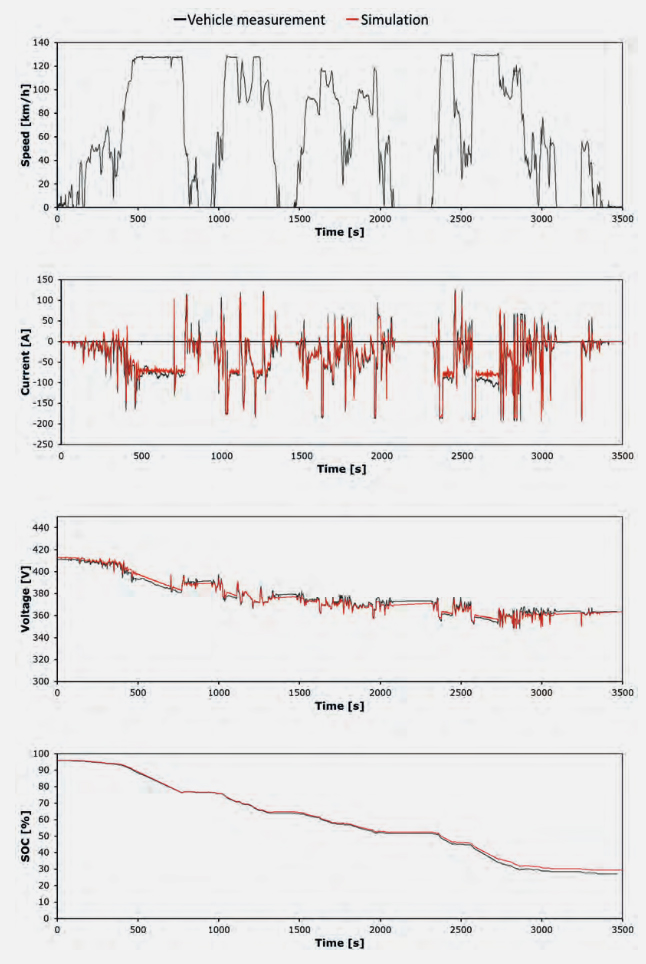
Figure 2: Simulation of a battery system embedded in the APL BEV-model and validation with measurement data.
In addition to the proper basic design, the performance of the overall system is highly dependent of how the system levels and components interact. Each battery cell in itself is a highly complex electrochemical system. All internal reactions and physical processes have their own dependencies on the influencing factors acting on them, such as temperature. This often results in a complex interplay of overlapping effects, the sum of which influences the macroscopic cell and system behavior, Figure 3. There, the dependence of the battery internal resistance was measured on a BEV for benchmark purposes. The influences of State of Charge (SoC) and temperature are clearly visible.
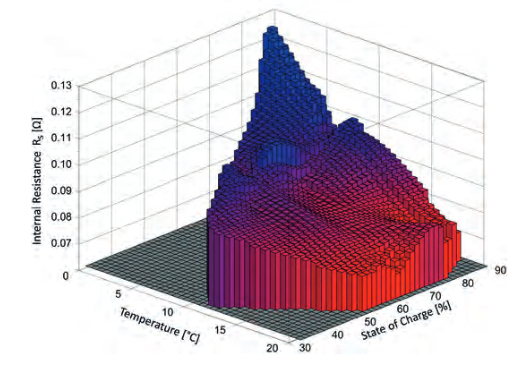
Figure 3: Impact of the parameters State of Charge and temperature on the internal resistance of a battery system in a vehicle
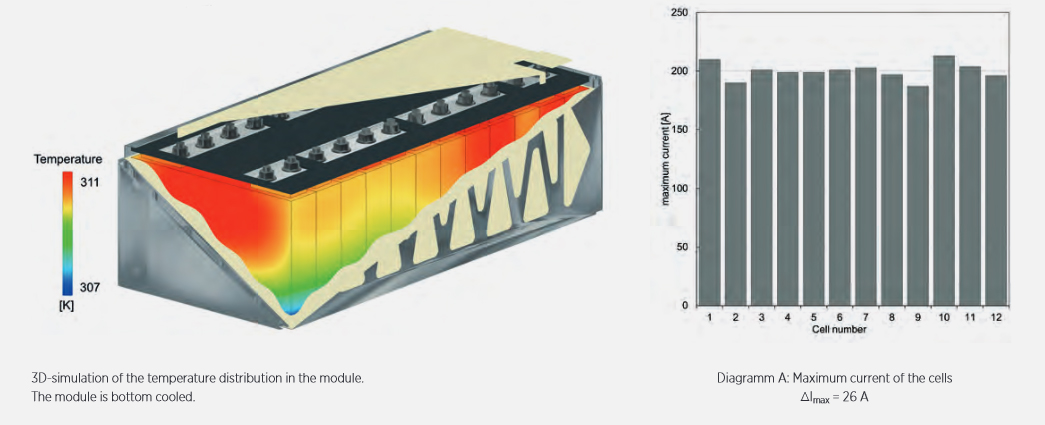
When connecting several hundred cells, individual effects can be further amplified. Therefore, the APL Cell-to-Pack model describes each single cell, with their respective characteristics, in the simulation of a battery pack accordingly. Specific system properties and cell-to-cell variations can lead to local hot or cold spots, strong current peaks and drifts in the state of charge, as the simulation results show, Figure 4. These effects strain the overall battery system and significantly increase the burden on particular cells: higher temperatures, higher current loads and more extreme states of charge. The cells show accelerated degradation which manifests as an increase in internal resistance and a loss of storage capacity. This can lead to a self-reinforcing effect. The performance of the total battery pack worsens due to the limitation of individual cells.
Figure 4: Simulation results of a battery module of 12 individual cells. The different characteristics of the cells lead to local hot- and cold-spots.
The illustration of the mutual interactions between the system levels makes it clear that a variety of measures and optimizations in the development and operation of the system are necessary in order to address the problem in a targeted manner. These extend to all levels of the battery system, starting with the choice of the appropriate cell in terms of chemistry, geometry and quality, the design of the circuit topology or the cooling system up to the operating and balancing strategies used. These questions are answered with the aid of suitable simulation models.
Relevance of thermal simulation
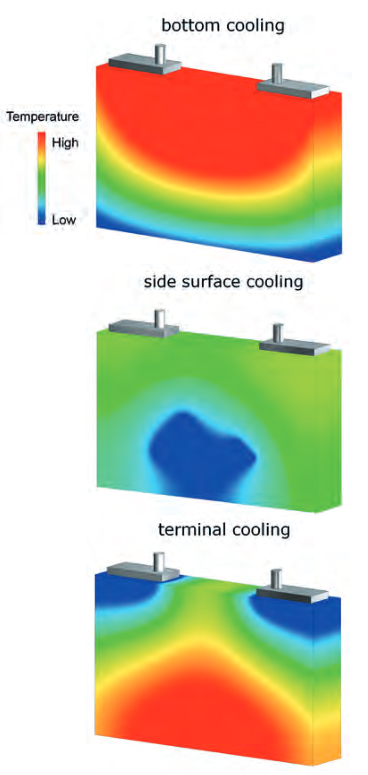Figure 5 shows the influence of different cooling concepts on the temperature distribution within the cell body. For example, in a cell cooled from below, large temperature differences occur over the height. Depending on the cell geometry, these can amount to several Kelvin. In the warmer cell regions, the electrochemical transport processes are favored; consequently, this part of the cell is more efficient and thus also more electrically stressed. Due to the increased thermal and electrical stress, the cell will age above average in this area. Nevertheless, the bottom cooling remains a widely used cooling concept. It offers significant advantages in terms of economic and safety aspects. To assess the consequences of the thermal management and to develop the right cooling strategy, APL uses a combination of 3D electro-thermal simulations with spatially resolved aging models. CFD calculations are used for the design of the cooling channels.
Basic prerequisite for all above mentioned simulations and design studies is an adequate depiction of the battery cell as the core element. The models used differ in their underlying scientific, technical or mathematical content. The approaches employed at APL can be broadly categorized into the three following types.
Figure 5: Simulation for investing the temperature distribution over the cell body when using different cooling concepts.
n addition, other physical phenomena such as thermal effects, volume changes, material stresses or particle size distributions can be taken into account. The underlying electrochemical model is thus extended to a multi-physics model. Models of this category are used at APL to investigate novel problems such as new material compositions and structures inside the cell. At an even lower level is the field of molecular or atomistic models, which are used, for example, to study the behavior of lithium ions in the course of charge/discharge cycles. These modeling forms are applied to investigate the influence of different crystal structures on the lithium diffusion or to describe the Solid Electrolyte Interphase (SEI) formation on the surface of the electrode particles.
Examples for physicochemical models:
- single particle models to describe the transport processes within a single active material particle of the electrode
- pseudo-2D models, which depict all relevant cell components including current collectors, electrodes, electrolyte, and separator in a simplified way
- multi-dimensional multiphysics models to simulate the internal cell structures and the inclusion of other physical effects such as thermal or mechanical stresses as realistically as possible
In general, electrochemical and physical phenomena are considered, with a focus on lithium diffusion and intercalation. The models illustrate processes and parameters that are not accessible experimentally or only with great difficulty. The aim is to build a better understanding of the mechanisms inside a battery cell and to further optimize the cell design. Thus, this form of modeling is used in particular in cell development and optimization with regard to the selection of materials, the composition and the morphology of electrodes or electrolyte.
Based on basic models for describing individual phenomena, these are supplemented by further physicochemical effects and thus expanded to more complex models. The quality of the predictions made can be increased by the continuous expansion of the model, but at the expense of the computing time. A validation of the models with experimental data is usually only possible at the macroscopic
level. Many of the generated parameters are not directly measurable and are therefore not available for comparison.
The conflict between the level of detail and computational time means that even simpler battery models (for example single particle models) are used in research, provided that they are appropriate.
Equivalent circuit models
In the equivalent circuit models (ECM), an analogy to the battery is created that accurately reflects its electrical behavior. To do so, basic electrical components such as voltage sources, resistors and capacitors are utilized. With the appropriate constellation and parameterization of the components, these models can be applied in a variety of ways.
Examples for ECM:
- the Rint-model, which describes the battery simply by a voltage source and an internal resistance
- the Thevenin model, in which an additional Resistor/Capacitor (RC) element describes the dynamic transient response and the polarization
- the DP (Dual Polarization) model, where concentration polarization and electrochemical polarization are taken into account using two RC elements, Figure 6.
In this form of modeling, the focus is on reliably predicting the external electrical performance of the battery. From direct analogies of the components, correlations to the physical effects inside the cell can be possible to a certain extent. ECM are very flexible to use while remaining fairly computationally efficient. Therefore, equivalent circuit models can be used in real-time applications, such as inside the BMS. They are highly scalable for SoC calculations, adaptive methods (e.g., Kalman filters), and thermal models, and can be applied at the cell, module, or pack level. These key advantages make ECM an extremely popular tool for battery system development and BMS-driven battery operation. Parameterization of the models can be done via pulse tests or electrochemical impedance spectroscopy. APL uses a combination of both methods for optimal mapping of all time domains.
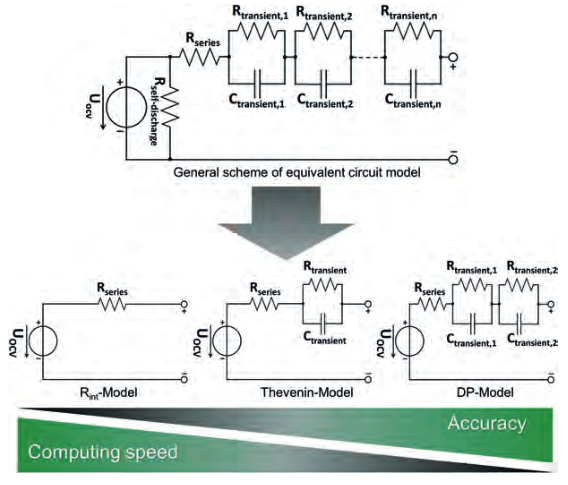
Figure 6: Schematic architecture of equivalent circuit models for battery simulation.
Empirical models and artificial intelligence
Unlike physical-chemical models, empirical models are not based on physicochemical principles but are purely mathematical approaches. They treat the battery cell as a black box. Based on extensive
measurement data, input and output variables are empirically linked. The required data sets are collected in APL’s large test lab for battery cells. With this data the models are trained in battery behavior.
Examples for empirical models:
- neural networks
- analytical terminal voltage models
- stochastic battery models
- fuzzy logic
This class of models is used in particular to model parameters and effects that are difficult or impossible to model physically. Empirical models are particularly popular in the field of aging simulation and lifetime prediction, since the sum of the physical-chemical processes occurring during battery aging is hardly predictable. In aging test series performed over several months, certain influencing parameters, such as the state-of-charge, the current rate or the depth of discharge, are varied under different thermal boundary conditions. Calendar and cycle aging effects can be evoked in isolation. At APL the data is used to train an artificial intelligence for battery state prediction [1].
Applying the models in the development process
Virtual models have become an irreplaceable tool in vehicle and battery development. With the help of simulations, requirements are broken down in a top-down approach from the vehicle requirement to the component and the physical-chemical phenomenon. For the HV battery a great variety of modeling approaches are available. Which is most appropriate depends largely on the application.
In electric powertrain development, equivalent circuit models or highly reduced physicochemical battery models are predominantly used. In cell development with respect to chemistry and materials, meanwhile, it is the physicochemical models that lead the way.
In order to address various engineering tasks and demonstrate the essential synergies from the battery cell to the battery pack, APL combines several models of different types and applies them together. In addition, regular experimental validation of the virtual predictions is performed to ensure the robustness of the results.
